The name Ada Lovelace (more formally, Augusta Ada King, Countess of Lovelace) is one that has become closely linked to early developments in computing. This is due to her collaboration with the nineteenth-century polymath Charles Babbage on designs for his proposed 'Analytical Engine', which we now recognise as a steam-powered programmable computer.
The precise nature of Lovelace’s contributions has seen a great deal of argument amongst scholars, with much of the debate focusing on whether she had the necessary mathematical background knowledge. In a recent book, Ada Lovelace: The Making of a Computer Scientist, we have argued, based upon mathematical manuscripts held by the Bodleian Library in Oxford, that she was indeed a competent mathematician, and fully capable of working with Babbage.
Babbage started work on his Analytical Engine in the mid-1830s, with the idea of creating a new calculating machine that could “eat its own tail”, by which he meant that it could modify its calculation while it was running. It would do this by pausing during a calculation, and using the values it had already determined to choose between two possible next steps. Babbage listed the basic operations that such a machine, with a large enough memory, would need if it were to execute “the whole of the developments and operations of analysis”, in other words any calculation that could be conceived of at the time. We now know that the basic operations that he described are what are needed to compute anything that can be calculated by any modern computer. This means that the Analytical Engine would have been, in modern terms, a general-purpose computer, a concept first identified by Alan Turing in the 1930s.
The Analytical Engine was never built, but many aspects of its design were recorded in immaculate detail in Babbage’s drawings and mechanical notation. It was to be programmed by means of punched cards, similar to those used in the weaving looms designed by Joseph Marie Jacquard. Separate decks of cards made up what we would now call the program, and gave the starting values for the computations. A complex mechanism allowed the machine to repeat a deck of cards, so as to execute a loop. The hardware involved many new and intricate mechanisms and was conceived on a massive scale. The central processing unit, which Babbage called the Mill, would be fifteen feet (4.5m) tall; the memory, or Store, holding a hundred 50-digit numbers would be twenty feet (6m) long (Babbage even considered machines with ten times that capacity); and other components included a printer, card punch, and graph plotter. Babbage estimated it would take three minutes to multiply two 20-digit numbers. A machine of that size would indeed have required steam power.

Disillusioned with what he saw as a lack of support from the British scientific establishment, Babbage looked for funding abroad. In 1840, Italian scientists invited him to Turin, where he lectured on the principles of the Engine. In the audience was Luigi Menabrea, who in October 1842 published the first account of the Engine, in French, based on Babbage’s lectures. Ada Lovelace had been thinking for some time about how she might contribute to Babbage’s projects. Another scientific friend, Charles Wheatstone, asked if she would translate Menabrea’s article, and Babbage suggested she expand it with a number of appendices.
After several months of furious effort by them both, the resulting paper was published in Taylor's Scientific Memoirs in August 1843. It was signed only with her initials, A.A.L., and of its sixty-six pages, forty-one make up her appendices.
The paper is most famous for the final appendix, Note G. This demonstrates the operation of the machine by giving the example of the calculation of the so-called 'Bernoulli numbers', which crop up in many places in modern mathematics. The Bernoulli numbers are particularly amenable to machine calculation because they are defined recursively: we may use the first to determine the second, the second for the third, and so on. There are several different ways of calculating these numbers, and Lovelace did not choose the simplest: she noted instead that the “object is not simplicity or facility of computation, but the illustration of the powers of the engine”.
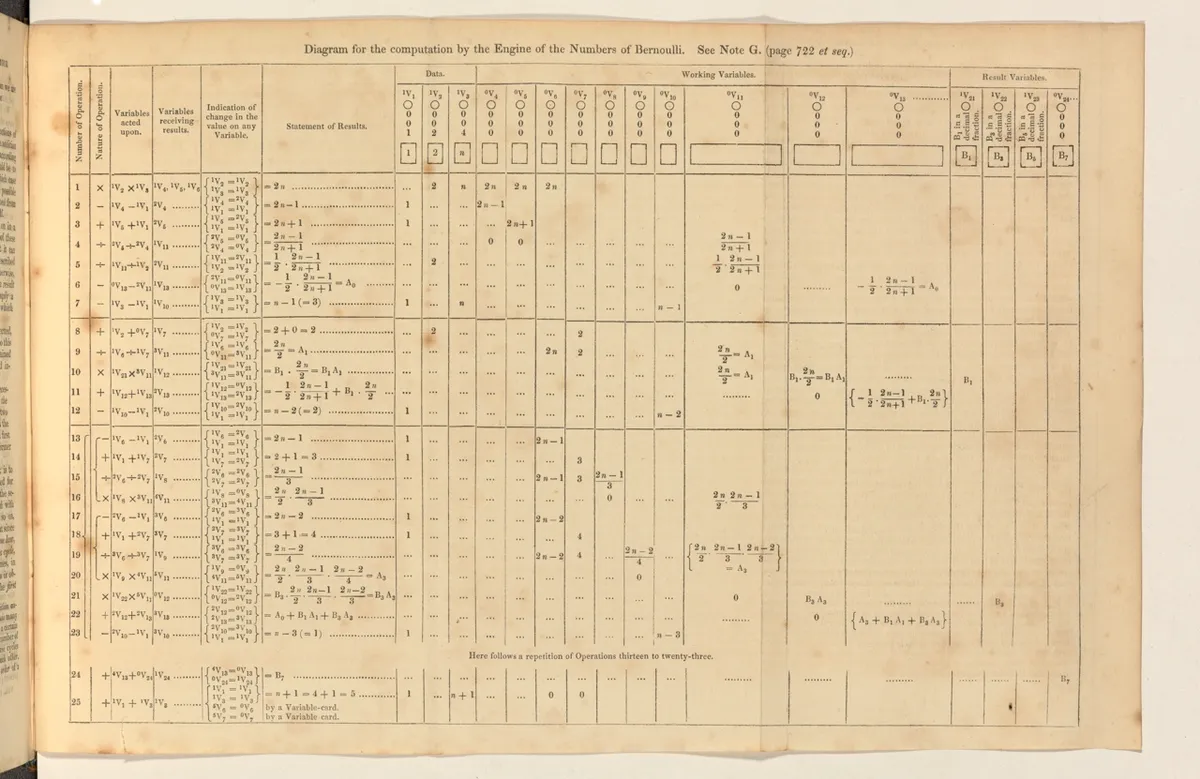
The paper contained a detailed explanation of how the various quantities involved in the computation of the Bernoulli numbers are fetched from the Store, used in calculation in the Mill, and moved back again, according to the instructions on the cards. The process is illustrated using a large table, whose columns represent the values of the data, the variables, and the intermediate results, as the engine carried out each stage of the calculation.
This table is often described as “the first computer program”, though Lovelace wrote, more accurately, that it “presents a complete simultaneous view of all the successive changes” in the components of the machine, as the calculation progresses. In other words, the table is what computer scientists would now call an “execution trace”. The “program”, had the idea existed at the time, would have been the deck of punched cards that caused the machine to make those successive changes. Babbage’s designs were rather unclear about aspects of how the cards would be manipulated, so it is hard to reconstruct the exact program. Such tables were still used as a method for explaining computation 100 years later, when Geoff Toothill drew a similar diagram to illustrate the working of the first stored program computer, the “Manchester Baby”.
'Note G' is the culmination of Lovelace’s paper, following many pages of detailed explanation of the operation of the Engine and the cards, and the notation of the tables. The paper shows Lovelace’s obsessive attention to mathematical detail – it also shows her imagination in thinking about the bigger picture.
Lovelace observed a fundamental principle of the machine, that the operations, defined by the cards, are separate from the data and the results. She observed that the machine might act upon things other than number, if those things satisfied mathematical rules. “Supposing”, she wrote:
“that the fundamental relations of pitched sounds in the science of harmony and of musical composition were susceptible of such expression and adaptations, the engine might compose elaborate and scientific pieces of music of any degree of complexity or extent.”
She thought about how the engine might do algebra, how it “weaves algebraical patterns just as the Jacquard loom weaves flowers and leaves”,and how it might make new discoveries; “We might even invent laws for series or formulæ in an arbitrary manner, and set the engine to work upon them, and thus deduce numerical results which we might not otherwise have thought of obtaining.”
These led her to think about what we now call artificial intelligence, though she argued that the engine was not capable of original ideas;“The Analytical Engine has no pretensions whatever to originate anything. It can do whatever we know how to order it to perform.”
Alan Turing disagreed. He wrote a famous paper on 'Computing machinery and intelligence', where he challenged what he called “Lady Lovelace’s objection” by suggesting that we can “order” the machine to be original, by programming it to produce answers that we cannot predict.
Lovelace’s thoughts about using the machine are very familiar to present-day programmers. She understood how complicated programming is, and how difficult it can be to get things right, as “[t]here are frequently several distinct sets of effects going on simultaneously; all in a manner independent of each other, and yet to a greater or less degree exercising a mutual influence.”
And, echoing a concern of every programmer ever, she also appreciated the need to “reduce to a minimum the time necessary for completing the calculation”.
Lovelace’s paper is an extraordinary accomplishment, probably understood and recognised by very few in its time, yet still perfectly understandable nearly two centuries later. It covers algebra, mathematics, logic, and even philosophy; a presentation of the unchanging principles of the general-purpose computer; a comprehensive and detailed account of the so-called “first computer program”; and an overview of the practical engineering of data, cards, memory, and programming.
Lovelace and Babbage’s collaboration by letter, as they exchanged versions of the table for the Bernoulli numbers, echoes the frustrations of all collaborators — “Where is it gone?” wrote Babbage, as they lost track of Note G. Towards the end of the work tempers became frayed. Lovelace refused to let Babbage add to the paper a strong criticism of the British government; and Babbage turned down her offer to become further involved in organising the building of the engine.

However Babbage continued to speak admiringly of Lovelace, writing to Michael Faraday of“that Enchantress who has thrown her magical spell around the most abstract of Sciences and has grasped it with a force which few masculine intellects (in our own country at least) could have exerted over it.”
They did not collaborate again, but remained friends: Lovelace’s letters to Babbage are full of details of the mathematics books she was reading, the progress of her children, and the antics of her dogs, chickens, and starlings. In the last year of her life, Babbage accompanied the now frail Lovelace to the Great Exhibition, and encouraged her to “put on worsted stockings, cork soles and every other thing which can keep you warm”. To his annoyance, none of his machines were displayed there.
This article is adapted from Chapter 7 of the book Ada Lovelace: The Making of a Computer Scientist byChristopher Hollings, Ursula Martin, and Adrian Rice (£20, Bodleian Library Publishing).
Follow Science Focus onTwitter,Facebook, Instagramand Flipboard