You know the Romans: a hard-nosed, humourless, our-marble-garbage-will-linger-here-for-millennia kind of people. In the year 212 BCE, their forces came to the Sicilian coast to conquer the stubborn little city of Syracuse.

As historian Polybius relates, they were armed to the teeth, in 60 ships “filled with archers, slingers, and javelin-throwers,” not to mention 4 huge boat-mounted siege ladders.

But Syracuse knew the old adage “When in Rome’s grip, do as the Romans do.” That is, fight like hell. And so, from catapults great and small, the Syracusans launched “immense masses of stone,” “large lumps of lead,” and a shower of iron darts.

Then, great mechanical claws emerged from the city walls and grabbed the Roman ships, which were thus “dashed against steep rocks” and “plunged…to the bottom of the sea.” The historian Plutarch narrates: “The Romans, seeing that infinite mischiefs overwhelmed them from no visible means, began to think they were fighting with the gods.”

Even worse. They were fighting with Archimedes.

In your office’s greatest-mathematician-of-all-time pool, Archimedes is a pretty solid first-round choice. Galileo called him “superhuman.” Leibniz raved that he spoiled genius itself, making later thinkers seem prosaic by comparison. “There was more imagination in the head of Archimedes,” Voltaire wrote, “than in that of Homer.”

Admittedly, he never won a Fields Medal, maths' most celebrated prize, but in Archimedes’s defence, his face is the one on the medallion.

You want a sense of his cleverness? Here: take a cube and cut it into three equal pieces.

The three pieces are identical pyramids, each with a square-shaped bottom and a pinnacle above one corner of the base. Therefore, each must occupy exactly 1/3 of the original cube’s volume.

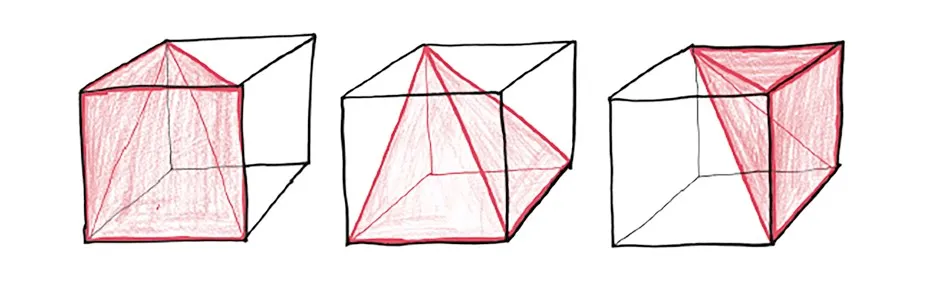
So far, so nifty. But we’re just getting started.

Take one of those pyramids and dice it up into infinite slices, each infinitesimally thin. If I’ve done this right—and, given my clumsiness with ordinary kitchen knives, you may want to double-check my work with this infinite conceptual knife—every cross-section should be a perfect square.

The very bottom square fills the whole base of the cube. The very top one is so tiny that it’s just a single point. Between these extremes lie squares of intermediate size.

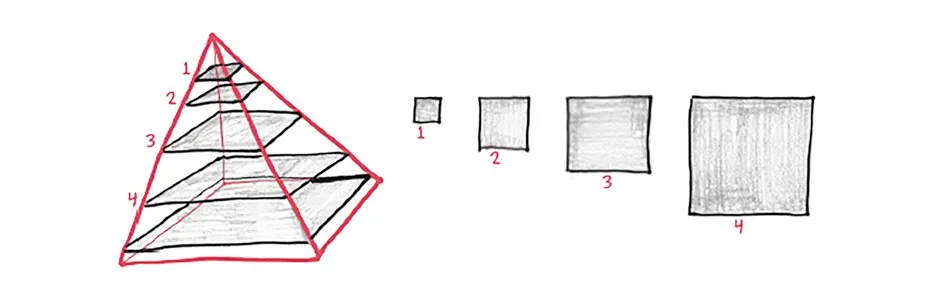
Now, turn up the heat further. Imagine those squares as a stack of infinite cards, each shadow-thin. Rearranging them won’t change the volume of the stack, so let’s get shuffling. At the moment, our squares share a common corner. But why not nudge them over, so that they share a common centre? This renovates our funky asymmetric pyramid into a classic Egyptian-style one.

Best of all, the volume doesn’t change. It remains 1/3 of the cube.

Read more about great scientists:

Alan Turing’s legacy should be for his triumphs, rather than his tragedy
Helen Gwynne-Vaughan: An extraordinary botanist whose problems of identity still confront female scientists today

We arrive now at a move so ingenious and handy that, when mathematician Bonaventura Cavalieri rediscovered it 1800 years later, they’d dub it “Cavalieri’s principle” in his honour.

In reality, it originated with Antiphon (5th century BCE), grew with Eudoxus (4th century BCE—in fact, he first gave the argument I’m giving now), and reached masterful heights with Archimedes (3rd century BCE—we’ll get to his singular contributions soon). I’m going to call it, in honour of Roman panic, “the Principle of Infinite Mischiefs.”

The idea is simple. In a 3D shape, you don’t affect the volume when you swap out cross-sections for others with equal area. For example, we can cash in our squares for rectangles. The now-elongated pyramid still fills 1/3 of the Prism Formerly Known as Cube.

Or—the grand master’s endgame—we can turn those squares into circles. Never mind that actually doing this with pencil and paper is called “squaring the circle,” and is, in hands-on terms, impossible. “Hands-on” is for gymnasts; we’re gliding through the clouds of pure geometry. So just imagine each square slowly morphing into a circle, its area never changing.

Our pyramid becomes a cone. Our cube becomes a cylinder. And thus, a cone fills 1/3 of the cylinder that contains it.

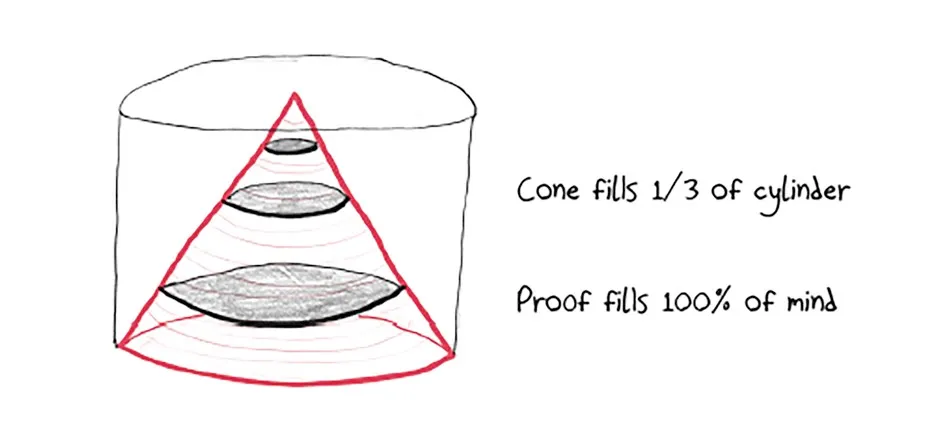
Pretty cool, right? In the second century, Plutarch gushed:

It is not possible to find in all geometry more difficult and intricate questions, or more simple and lucid explanations… No amount of investigation of yours would succeed in attaining the proof, and yet, once seen, you immediately believe you would have discovered it; by so smooth and so rapid a path [Archimedes] leads you to the conclusion required.

Still, these geometric excursions don’t exactly scream “military genius.” One has to wonder: Where did his Rome-battering war engines come from?

“These machines he had designed and contrived,” Plutarch insists, “not as matters of any importance, but as mere amusements in geometry.” Peculiar as that sounds, it’s a basic pattern of mathematical history. An aimless flight of fancy leads, somehow and someway, to a technological breakthrough down the road.

Although the Romans didn’t much appreciate pure mathematical inquiry, they sure appreciated boat-crushing death claws. Recognising themselves as the villains in an ancient prequel to Home Alone, General Marcellus and his forces retreated.

Read more about maths:

One afternoon, several months later, Archimedes was scratching diagrams in the dust. I like to imagine he was revisiting his favourite proof—the theorem that he instructed friends and family to commemorate upon his tomb.

It begins with a sphere.

We encase it in a cylinder, so that the fit is perfect and snug, like a single serving of tennis ball.

Archimedes’s question was this: What fraction of the cylinder does the sphere fill?

(Really, his question was more elemental: How big is a sphere? But any description of size requires reference to something already known—e.g., my height is approximately 5 2/3 of those preexisting units called feet—and that’s where the cylinder comes in.)

To begin, cut the whole shape in half. Instead of a tennis ball in a snug container, we’ve got a hemisphere in a hockey puck.

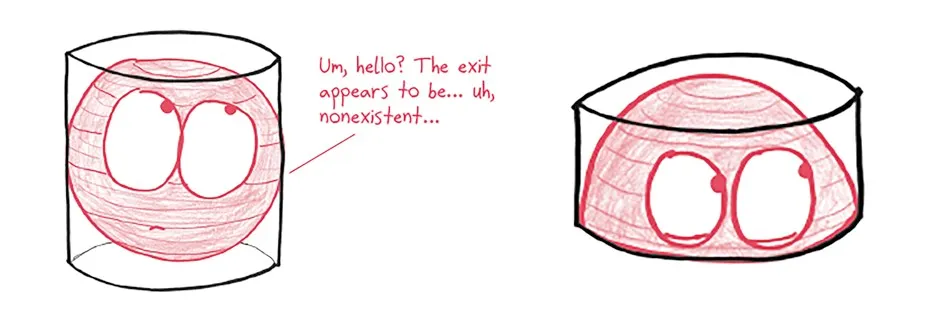
Now, instead of worrying about the volume inside the hemisphere, we’re going to focus on the volume outside of it. In the spirit of Infinite Mischiefs, we can think of this region as a stack of hoops or washers. Each is a circle with a circular hole cut out.

At the bottom of this stack is a superthin washer. Its hole occupies the whole circle, leaving just a stringlike ring. At the top, meanwhile, is a superthick washer. It’s pretty much an intact circle with a pinprick aperture. In between is a whole family of intermediate washers.

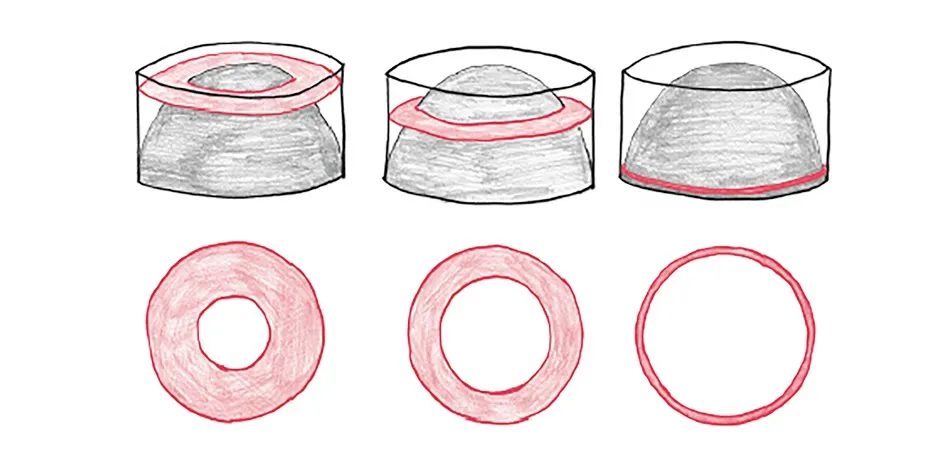
What are the areas of these shapes? With an interlude of slick algebra, we deduce that each has an area of πh², where h is its distance above the ground.

This means, invoking the Principle of Infinite Mischiefs, that each can be replaced with a circle of radius h.

Behold! What remains is no longer a strange hemisphere-shaped crater, but instead, a simple upside-down cone.

As we’ve already established, the cone fills 1/3 of the cylinder. Thus, the empty space—i.e., what used to be the hemisphere—fills 2/3.

Conclusion: the sphere fills 2/3 of the cylinder.

Learn more maths in theScience Focus Podcast:

With these diagrams in the Sicilian sand, Archimedes was dreaming of integrals, millennia in advance. Areas and volumes, infinite slices, rearrangements that solve problems of continuity and curvature: these are the chemical ingredients, the primordial soup, from which the integral would later develop. Why, then, would the world wait so long for calculus’s birth?

That day, Rome breached the city. Within hours, Syracuse burned, and soldiers ran amok, looting and killing. “Many brutalities were committed in hot blood and the greed of gain,” wrote the historian Livy. Still, the Roman leader Marcellus insisted that the great geometer be spared, “putting almost as much glory in saving Archimedes,” says another historian, “as in crushing Syracuse.”Archimedes didn’t even notice the city’s fall. What’s a little plunder and destruction, compared to the engrossing beauty of a figure in the dust?

Historians differ on what Archimedes said when a Roman soldier confronted him. Perhaps he begged: “Please, do not disturb my circles.” Perhaps he blustered: “Stand away, fellow, from my diagram.” Perhaps he shielded the dust with his hands, as if his ideas were more precious than his life: “Let them come at my head, but not at my line!”

In any case, sources agree that the soldier slew him. His blood filled the grooves that his fingers had traced. General Marcellus insisted on a proper burial, and honoured Archimedes’s relatives with gifts and favours. But the man of Infinite Mischiefs was dead.

Today, Archimedes’s greatest legacy lies not in catapults and claws, but in geometry. His lucid arguments, his grasp of infinity, how close he came to calculus. Could a little extra nudge have brought him there? Could calculus have emerged on Earth millennia earlier than it did?

Consider the testimony of mathematician Alfred North Whitehead:

The death of Archimedes by the hands of a Roman soldier is symbolical of a world-change of the first magnitude: the Greeks, with their love of abstract science, were superseded in the leadership of the European world by the practical Romans.

Nothing wrong with practicality. Or is there? Nineteenth-Century British prime minister Benjamin Disraeli defined a practical man as one “who practices the error of his forefathers.” According to Whitehead, that’s just what the Romans did. Nowhere in the vanquishing civilisation could you find the imaginative spark of the vanquished.

All their advances were confined to minor technical details of engineering. They were not dreamers enough… No Roman lost his life because he was absorbed in the contemplation of a mathematical diagram.

Centuries later, when the local Syracusans had all but forgotten Archimedes’s legacy, the writer Cicero set out in search of his grave. He found it “hidden by bushes of brambles and thorns”: “a little column, just visible above the scrub.”

He recognised it by the carving on top, just as Archimedes had requested: a sphere and a cylinder. The grave has long since vanished, but the proof remains etched in our collective imagination—a medium that can outlast dust, or blood, or all the stonework of Roman hands.

Change Is the Only Constant by Ben Orlin is out now (£20, Little, Brown).