Everything you need to know about quantum physics (almost)

What is quantum physics?

Quantum physics is a branch of physics also known as quantum mechanics or quantum theory.

Mechanics is that part of physics concerned with stuff that moves, from cannonballs to tennis balls, cars, rockets, and planets. Quantum mechanics is that part of physics which describes the motions of objects at molecular, atomic, and sub-atomic levels, such as photons and electrons.

Although quantum mechanics is an extraordinarily successful scientific theory, on which much of our modern, tech-obsessed lifestyles depend, it is also completely mad.

Read more about quantum physics:

• The parallel worlds of quantum mechanics
• Quantum field theory: "An unholy crossbreed between quantum physics in a bad mood and every button you never push on a calculator"
• Dead and alive: why it's time to rethink quantum physics

The theory quite obviously works, but it appears to leave us chasing ghosts and phantoms, particles that are waves and waves that are particles, cats that are at once both alive and dead, lots of seemingly spooky goings-on, and a desperate desire to lie down quietly in a darkened room.

If you’ve ever wondered what is it about quantum theory that makes it so baffling to many, here’s a brief summary of quantum in simple terms.

The history of quantum mechanics

We now know that all matter is composed of atoms. Each atom is in turn made up of electrons ‘orbiting’ a nucleus consisting of protons and neutrons. Atoms are discrete. They are ‘localised’: ‘here’ or ‘there’.

But towards the end of the 19th Century, atoms were really rather controversial. In fact, it was a determination to refute the existence of atoms that led the German physicist Max Planck to study the properties and behaviour of so-called ‘black-body’ radiation.

What he found in an ‘act of desperation’ in late-1900 turned him into a committed atomist, but it took a few more years for the real significance of his discovery to sink in.

Planck had concluded that radiation is absorbed and emitted as though it is composed of discrete bits which he called quanta. In 1905, Albert Einstein went further. He speculated that the quanta are real – radiation itself comes in discrete lumps of light-energy. Today we call these lumps photons.

Is light a wave or a particle?

Einstein’s hypothesis posed a bit of a problem. There was an already well-established body of evidence in favour of a wave theory of light. The key observation is called the 'double slit experiment'.

Push light through a narrow aperture or slit and it will squeeze through, bend around at the edges and spread out beyond. It ‘diffracts’.

Cut two slits side-by-side and we get interference. Waves diffracted by the two slits produce an alternating pattern of light and dark bands called interference fringes. This kind of behaviour is not limited to light – such wave interference is easily demonstrated using water waves.

But waves are inherently delocalised: they are ‘here’ and ‘there’. Einstein’s hypothesis didn’t overturn all the evidence for the delocalised wave-like properties of light. What he was suggesting is that a complete description somehow needs to take account of its localised, particle-like properties, too.

So, light acts like both a wave and a particle.

In 1923, French physicist Louis de Broglie made a bold suggestion. If light waves can also be particles, could particles like electrons also be waves? This was just an idea, but he was able to use it to develop a direct mathematical relationship between an electron’s wave-like property (wavelength) and a particle-like property (momentum).

But this was not a fully-fledged ‘wave-particle’ theory of matter. That challenge fell to Erwin Schrödinger, whose formulation – first published early in 1926 and called wave mechanics – is still taught to science students today.

What is a wave function?

Schrödinger’s theory is really the classical theory of waves in which we introduce some quantum conditions using de Broglie’s relation. The result is Schrödinger’s wave equation, in which the motion of a particle such as an electron is calculated from its wave function.

Right from the very beginning, physicists were scratching their heads about Schrödinger’s wave function.

In classical mechanics, there are no real issues with the way we interpret the concepts represented in the theory, such as energy and momentum (which are called physical observables) and their relation to the properties of the objects that possess them.

Read more about the quantum world:

• Quantum cryptography in a box of chocolates
• The quest for quantum gravity: why being wrong is essential to science

Want to calculate the classical momentum of an object flying through the air at a fixed speed? Easy. Measure the object’s mass and its speed and multiply these together. Job done.

But what if you want to know the momentum of an electron moving freely in a vacuum? In quantum mechanics we calculate this by performing a specific mathematical operation on the electron’s wave function.

Such operations are mathematical recipes, which we can think of as ‘keys’ which unlock the wave function (depicted in this animation as a box), releasing the observable before closing again.

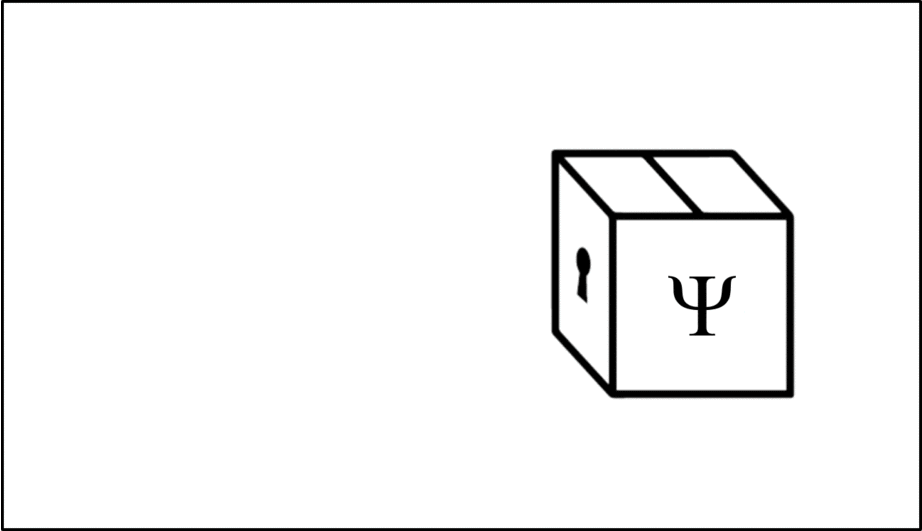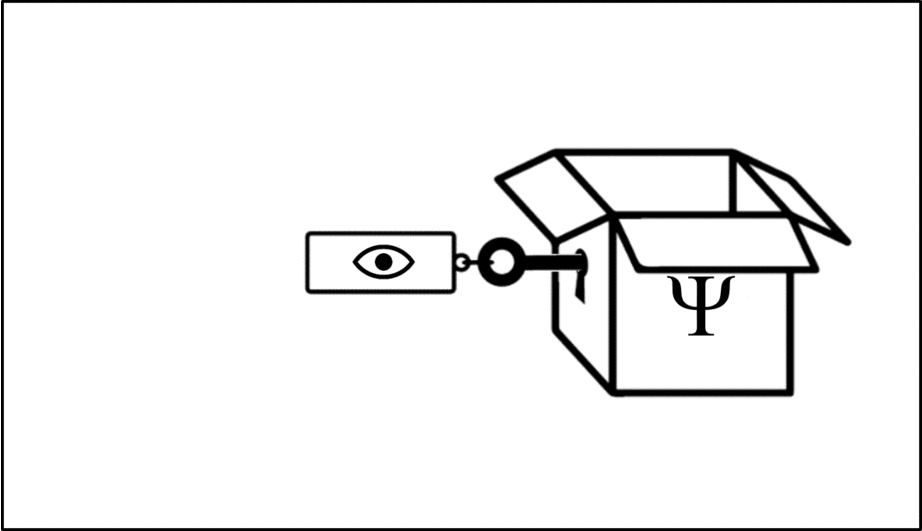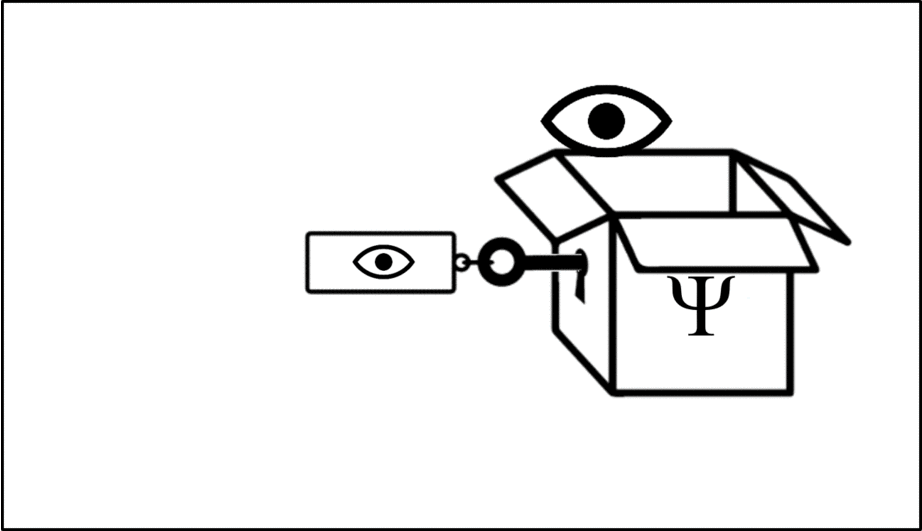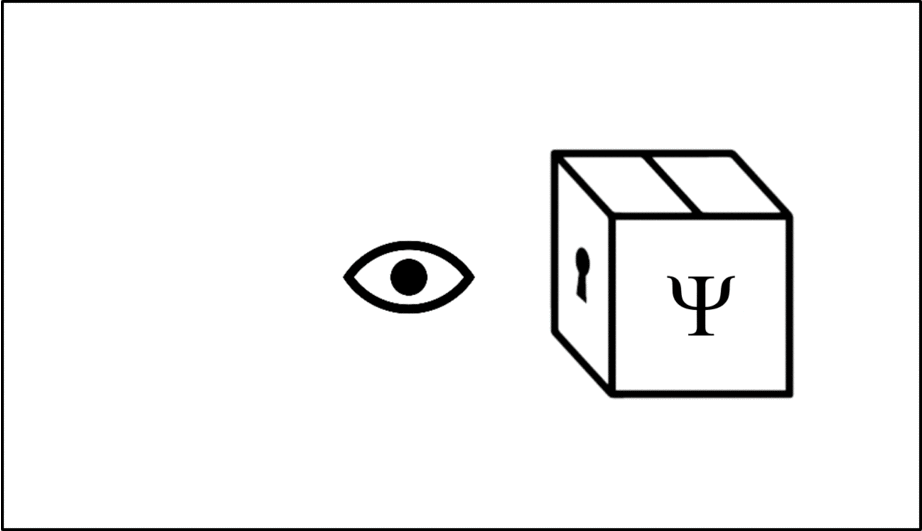
We calculate the momentum by opening the box using the ‘momentum key’. A different observable will require a different key.

Do particles really behave like waves?

So, if electrons behave like waves, can they be diffracted? If we push a beam of electrons through two slits side-by-side will we see interference fringes on a distant screen? What if we limit the intensity of the beam so that, on average, only one electron passes through the slits at a time. What then?

What we see is at first quite comforting. Each electron passing through the slits registers as a single spot on the screen, telling us that ‘an electron struck here’. This is perfectly consistent with notion of electrons as particles, as it seems they pass – one by one – through one or other of the slits and hit the screen in a seemingly random pattern.

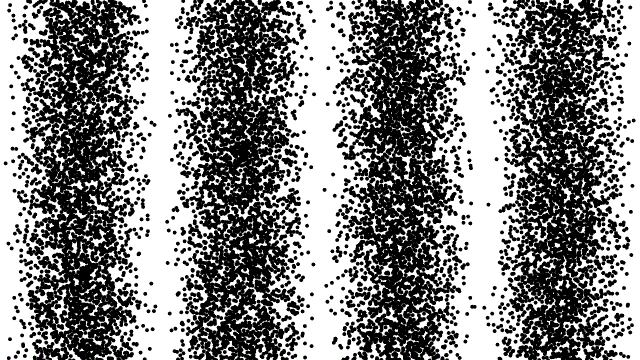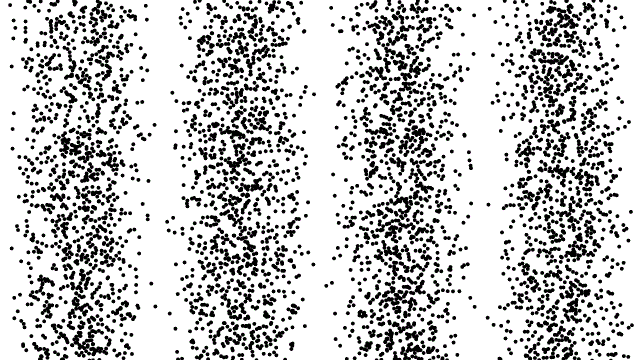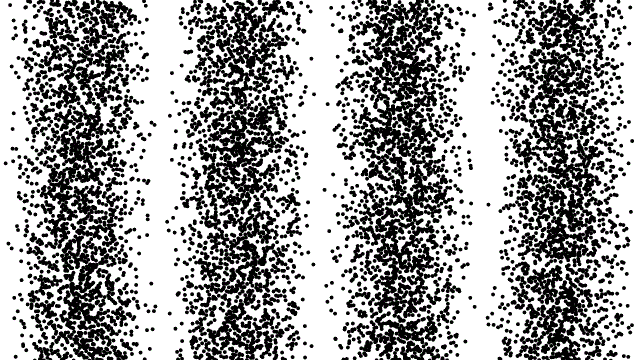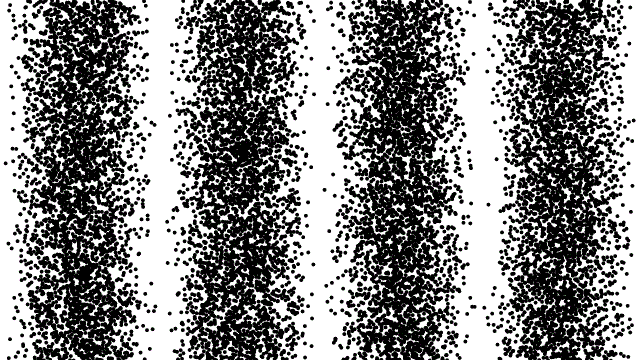
But wait. The pattern isn’t random. As more and more electrons pass through the slits we cross a threshold. We begin to see individual dots group together, overlap and merge. Eventually we get a two-slit interference pattern of alternating bright and dark fringes.

Alternatively, we conclude that the wave nature of the electron is an intrinsic behaviour. Each individual electron behaves as a wave, described by a wave function, passing through both slits simultaneously and interfering with itself before striking the screen.

So, how are we supposed to know precisely where the next electron will appear?

Can a particle be in two places at once?

Schrödinger had wanted to interpret the wave function literally, as the theoretical representation of a ‘matter wave’. But to make sense of one-electron interference we must reach for an alternative interpretation suggested later in 1926 by Max Born.

Born reasoned that in quantum mechanics the wave function-squared is a measure of the probability of ‘finding’ its’ associated electron in a certain spot.

The alternating peaks and troughs of the electron wave translate into a pattern of quantum probabilities – in this location (which will become a bright fringe) there’s a higher probability of finding the next electron, and in this other location (which will become a dark fringe) there’s a very low or zero probability of finding the next electron.

Read more about physics:

• What’s the most abundant particle in the Universe?
• What is rocket science?

Before an electron strikes the screen, it has a probability of being found ‘here’, ‘there’ and ‘most anywhere’ where the square of the wave function is bigger than zero. This probability of many states existing at the same time is known as 'quantum superposition'.

Does this mean that an individual electron can be in more than one place at a time? No, not really. It is true to say that it has a probability of being found in more than one place at a time. And, if we want to interpret the wave function as a real physical thing, there is a sense in which this is delocalised or distributed.

But if by ‘individual electron’ we’re referring to an electron as a particle, then there is a sense in which this doesn’t exist as such until the wave function interacts with the screen, at which point it ‘collapses’ and the electron appears ‘here’, in only one place.

Why is probability important in quantum physics?

One more thing. That there’s a 50 percent probability that a tossed coin will land ‘heads’ simply means that it has two sides and we have no way of knowing (or easily predicting) which way up it will land. This is a classical probability born of ignorance.

We can be confident that the coin continues to have two sides – heads and tails – as it spins through the air, but we’re ignorant of the exact details of its motion so we can’t predict with certainty which side will land face up. In theory, we could, if we knew exactly how hard you flipped it at exactly what angle, and at exactly what height you would catch it.

Quantum probability is thought to be very different. When we toss a quantum coin we might actually be quite knowledgeable about most of the details of its motion, but we can’t assume that ‘heads’ and ‘tails’ exist before the coin has landed, and we look.

So, it doesn't matter exactly how much information you have about the coin toss, you will never be able to say with any certainty what the result will be, because it's not pre-determined like in a classical system.

Einstein deplored this seeming element of pure chance in quantum mechanics. He famously declared that: ‘God does not play dice’.

And then, in 1927, the debates began. What is the wave function and how should it be interpreted? What is quantum mechanics telling us about the nature of physical reality? And just what is this thing called reality, anyway?