8 maths hacks to master Christmas

Tis the season to be jolly, but the stress of buying and wrapping Christmas presents, throwing the perfect Xmas party and decorating your tree shouldn’t leave you getting your tinsel in a twist. We sent our festive elves on a Yuletide mission to find the science hacks to make this year the perfect Christmas.

You have a long list of family and friends, but only limited funds in the bank. Who should you buy presents for?

Prof Rachel Norman and Dr Anthony O’Hare, at the University of Stirling, have applied game theoryto the exchange of gifts. Game theory is a branch of maths to do with calculating optimal strategies in competitive situations. Central to it is the idea of finding the unexploitable ‘Nash equilibrium’. If two people are both playing the Nash strategy, then neither can improve their lot by changing tack.

Let’s say receiving a present invokes enjoyment, E, but giving incurs cost, C. The diagram above shows the possible payoffs for two people. For example, if player 1 gives but player 2 doesn’t then player 1 gets -C_1 (a net cost) while player 2 has no cost but gets enjoyment E_2.

Read more:

• What happens to your body after eating Christmas dinner?
• How fast would Father Christmas have to fly to visit every child in the world?

The Nash equilibrium here is for both players to not give. The payoff for each is then zero – and if either one deviates unilaterally they become worse off.

This assumes that the ‘game’ is only played once. American political scientist Robert Axelrod has shown that when games are played many times, greedy strategies like this are no longer optimal. Instead, the best payoff comes from a ‘tit-for-tat’ approach – buying a present on the first Christmas and then, in subsequent years, copying what the other person did last time.

If you’re tired of forcing down dried up Christmas cake in March, then the good news is science has found a simple way to keep cake fresher for longer.

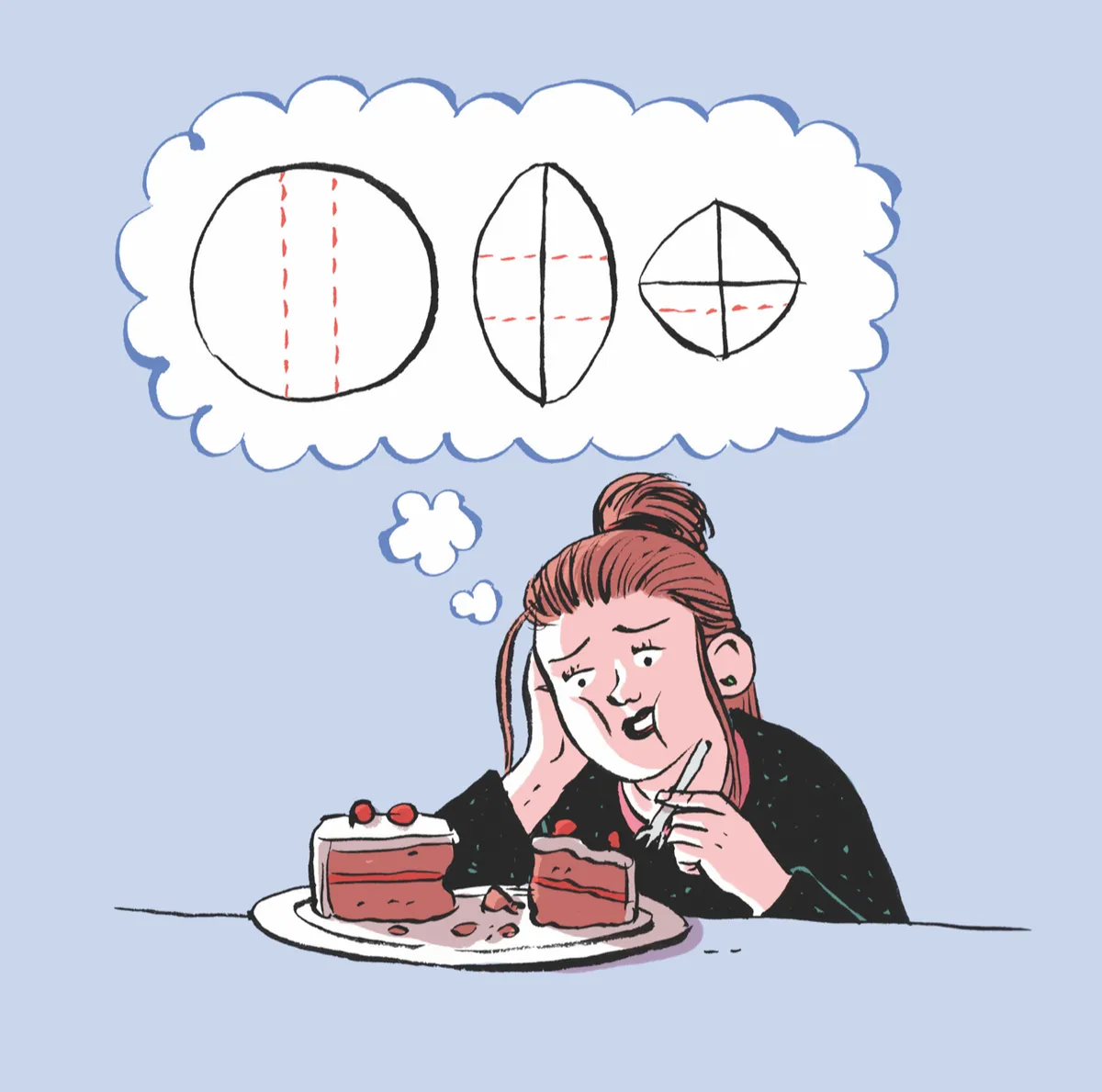
In a letter to the research journal Nature, published on 20 December 1906, the British polymath Sir Francis Galton opined that the traditional way of cutting a Christmas cake was “very faulty”. He argued that taking a wedge out at a time leaves the inside surface of the cake exposed and liable to get dry. Instead, Galton advocated a novel method of cake slicing that involves making parallel cuts through the centre of the cake and then closing it up and securing with an elastic band to lock in the freshness.

This is shown in the diagram, adapted from a sketch that accompanied Galton’s original letter. Solid lines show existing cuts; dotted lines show the next cut to make. The first cut, shown on the left, removes a flat slice and the cake is then closed up into an oval shape and stored. The next slice is removed in a similar fashion but at 90 degrees to the first cut, as shown in the centre image. The next slice would be taken parallel to the first cut and so on.

“The method works,” says maths writer Alex Bellos. “I have done it many times.”

What makes the perfect Christmas turkey?

Roasting a turkey is tricky because the meat is made up of different components that all, ideally, require cooking at different temperatures. For example, the breast meat shouldn’t be heated much above 55°C, to prevent it becoming too tough – whereas the darker leg meat needs to reach at least 80°C and the skin requires as much as 200°C to trigger the Maillard reactions that brown the outside and create the characteristic flavour.

Prof Peter Barham, a gastronomically inclined physicist at the University of Bristol, says the ideal strategy is to chop up the turkey and cook each part separately at its optimum temperature. In case a heap of slivered turkey flesh isn’t quite the table centrepiece you were hoping for, he suggests cladding the more sensitive parts in foil for the bulk of the roasting time.

But how long should that time be? The late Stanford University physicist Wolfgang Panofsky used the laws of heat conduction to come up with the formula t = 1.13 x W(2/3) where t is the cooking time in hours and W is the weight of the turkey in kilograms. He assumed an oven temperature of 165°C – and a spherical turkey.

For safety, it’s recommended to use a meat thermometer and ensure the inside of the bird is cooked to at least 75°C. Bon appetit!

Dr Sara Santos, of Goldsmiths, University of London, has devised a formula to calculate the optimal dimensions of wrapping paper to cover a cuboid box.

For a square-based box, you need a square of paper with side length equal to the base diagonal of the box plus 1.5 times its height. Place the box on the paper at 45 degrees, bring the corners of the paper up to meet at the top of the box and secure with a single piece of tape (fig 1). For a rectangular base, use a square of paper with side length equal to the width of the box plus its length plus twice its height, all multiplied by 0.75 (fig 2).

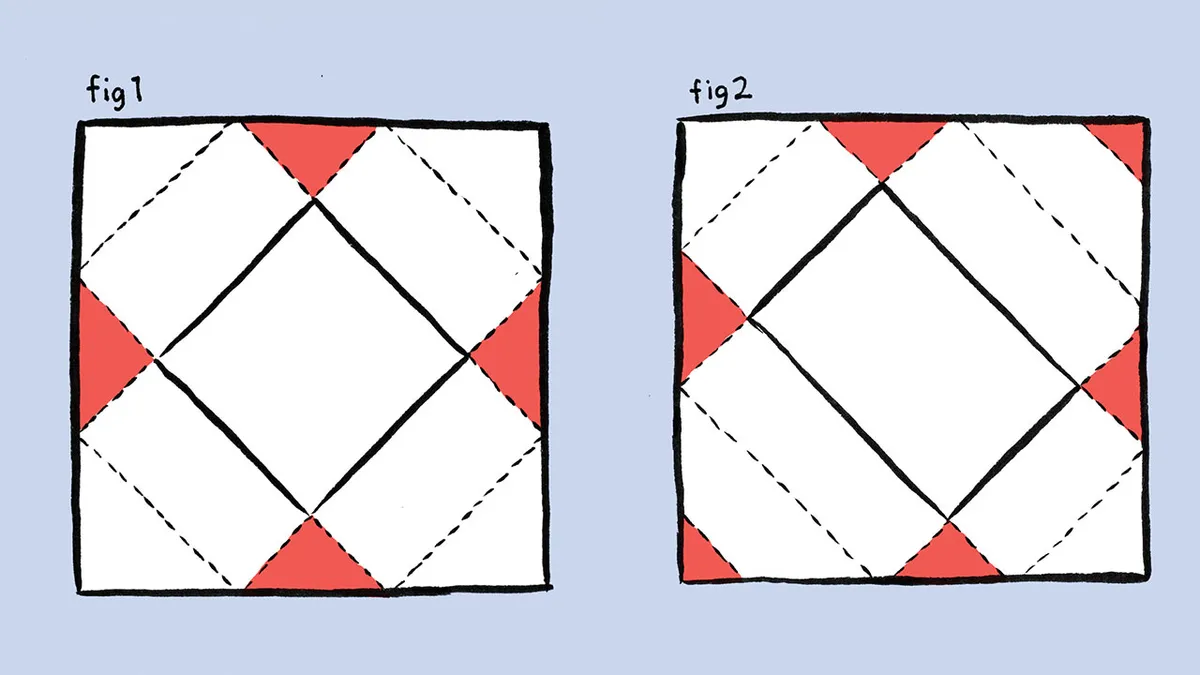
That said, Drs Hannah Fry and Thomas P Oléron Evans, in their bookThe Indisputable Existence of Santa Claus, argue that this technique uses no less paper than the traditional method – though it does look nice, and saves tape. They suggest a more practical approach is to use flatter boxes to minimise the paper wasted in flaps tucked in at the ends of the present. A box half as high as its base side length takes 11 per cent less paper than a cube of the same volume.

Taken to the limit, this means you should give totally flat presents – another reason to treat your nearest and dearest to copies of BBC Focus (nudge, nudge -subscribe here)!

In the office game of Secret Santa, people write their names on pieces of paper, put them in hat and then each draw one random person to buy a gift for. If anyone gets their own name, they replace it and draw again.

But this breaks down if the last person to draw picks their own name – in this case, to maintain anonymity, the only thing you can do is start over. And in an office of 10 people, this happens over 7.5 per cent of the time. It’s also not perfectly random.

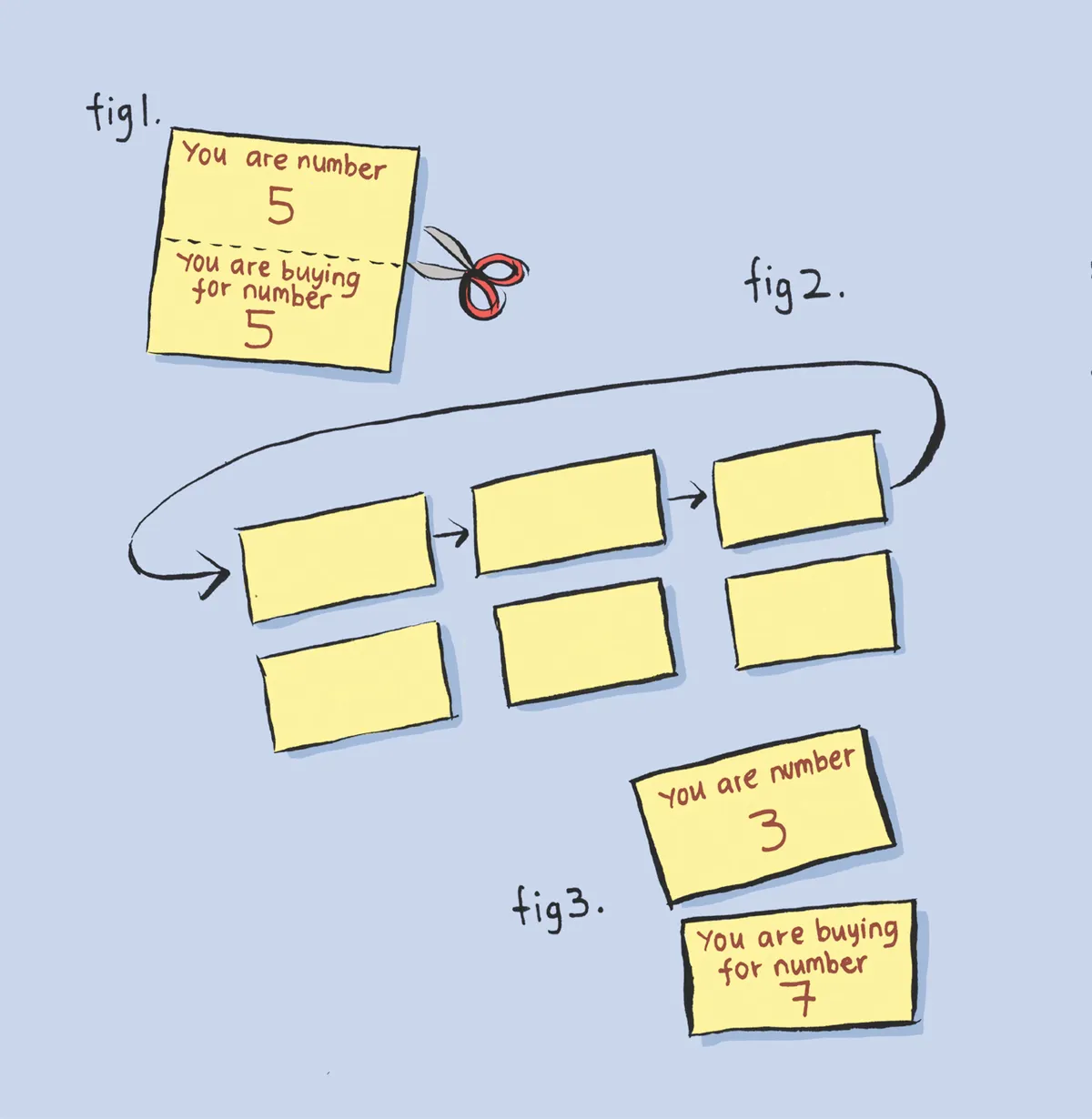
“If you’re last to pick in a group of three, then it’s twice as likely that the first picker is buying you a present than the second picker,” says Dr Hannah Fry. But she has a solution. Create a set of cards, one for each person. Each card should resemble fig 1. Place the cards face down in a row, shuffle and, keeping them face down, cut them in half. Now shift the cards on top one place to the right (fig 2).

Each person takes a card from the top row and the card directly below it – telling them their number and the number of the person they’re buying for (fig 3). Finally, you put a list of numbers on the wall and everyone writes their name next to their number. Such a draw is truly anonymous and perfectly random.

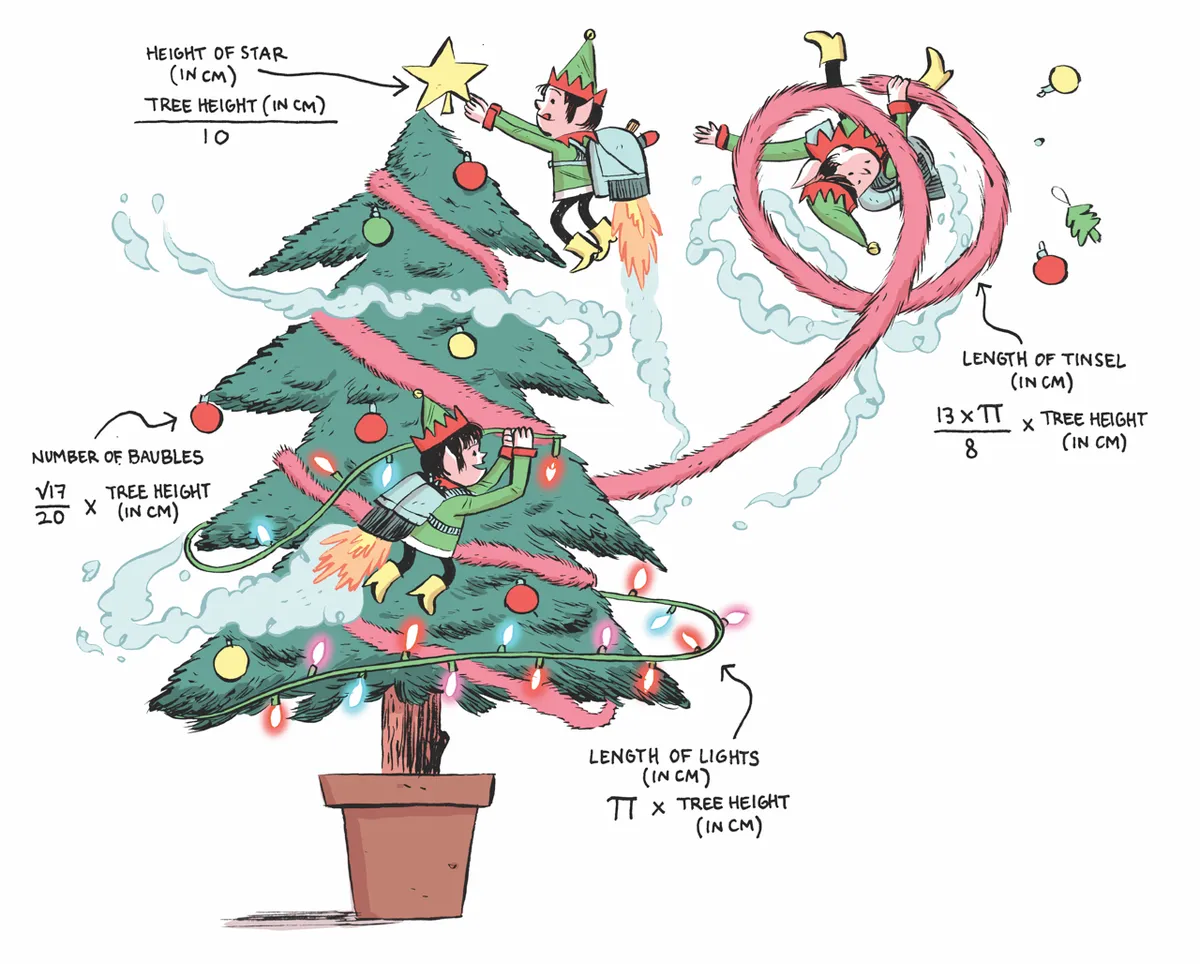
Students at the Sheffield University Maths Society (SUMS) have developed a set of equations to calculate the optimal amount of tinsel, number of baubles, length of lights and size of star with which to decorate your tree – all as handy mathematical functions of its height (you can test your own treehere). For example, if your tree is 152cm (5ft) tall, then the theory, which they call ‘treegonometry’, dictates that you should adorn it with 776cm of tinsel, 31 baubles and 478cm of lights – all topped off with a 15cm star.

But what about those perishing needles? One often-heard piece of advice is to add bleach to the water that the Christmas tree is stood in. However, when the Discovery Channel’sMythbustersteam tried this, the only thing they were able to confirm was that itturned the tree a funny colour.

A more promising strategy was uncovered by scientists at the Christmas Tree Research Centre (yes, really), at Dalhousie University, Nova Scotia. In 2016, they discovered that LEDs (especially red and white bulbs) give off the right spectrum of light to stimulate photosynthesis – enabling the tree to produce carbohydrates, giving it an energy source that keeps the needles attached to the tree for longer.

It’s also good news for the planet (and your pocket) as LED lights use 80 to 90 per cent less electricity than traditional filament bulbs. For more tips on keeping your tree looking spruce (sorry) read our interview with Prof Raj Lada, founder of the Christmas Tree Research Centre, inissue 316ofBBC Focus.

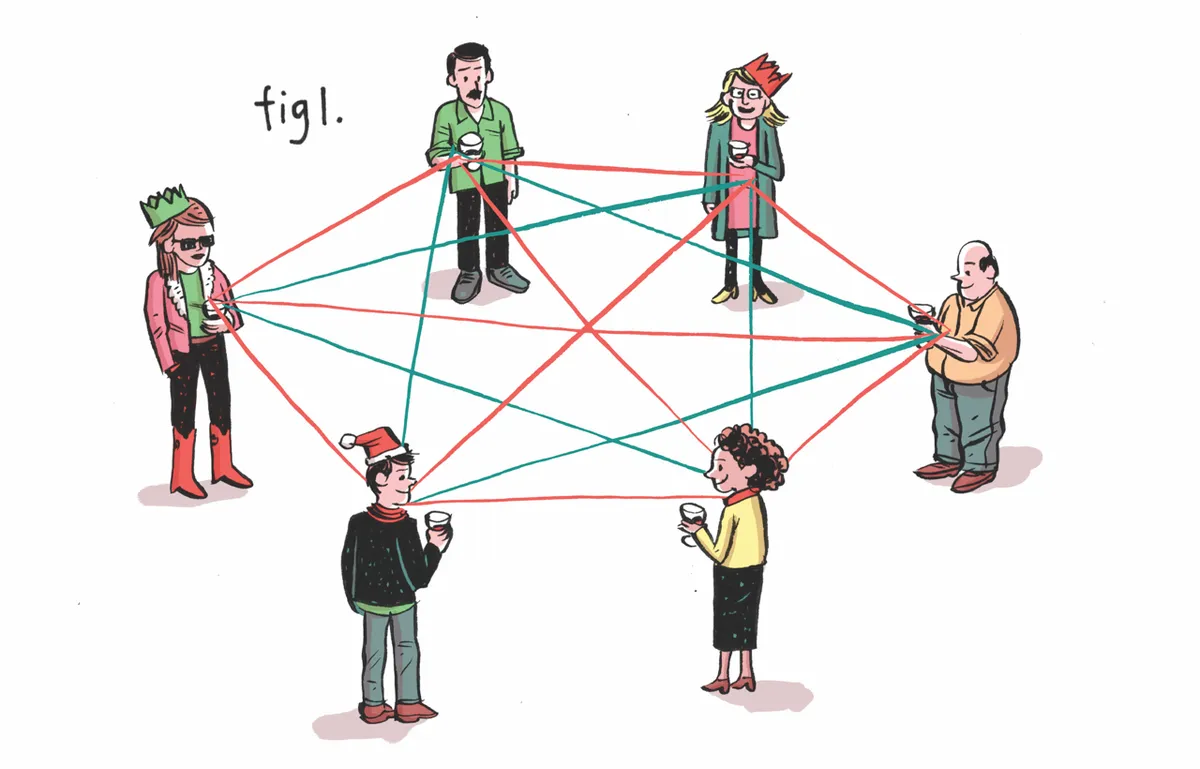
So you’re having people over at Christmas – but how many to invite? To encourage conversation, you want either three or more guests who are mutual strangers, or three or more who are already acquainted. So what’s the minimum number of people you need at the party to ensure this?

In 1928, British mathematician Frank Plumpton Ramsey found the answer with his theory on the connectedness of points on a graph. The ‘Ramsey numbers’ R(m, n) give the number of people to invite such that at least either m of them know each other, or n of them don’t. It turns out that R(3, 3) = 6.

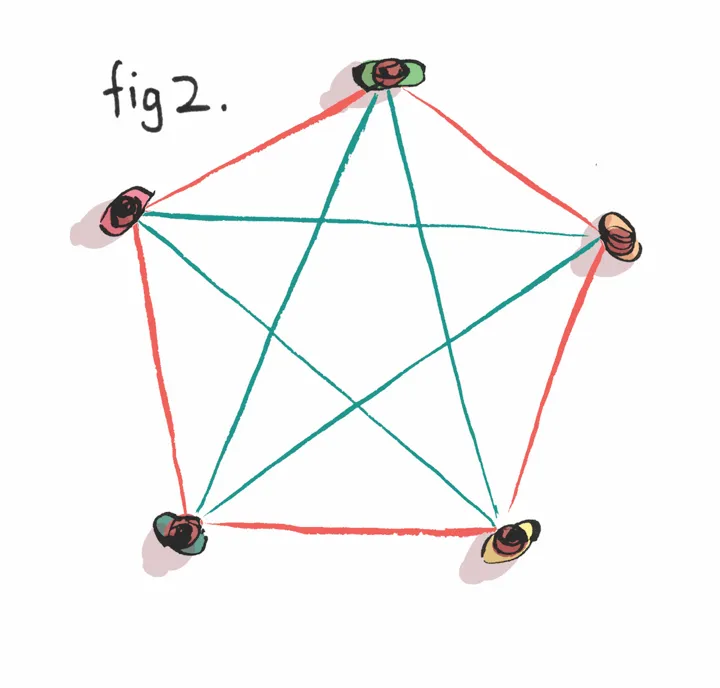
To see why, draw six dots on a sheet of paper, each representing a guest. Now draw lines from each guest to every other guest – red if they know each other, blue if they don’t. With six guests (fig 1) you’ll find it’s impossible to connect them all without creating either a red triangle (ie, three people who know each other) or a blue triangle (three people who are strangers). But this isn’t the case with just five dots (fig 2) – so six is the minimum number of people to invite.

Some more Ramsey numbers are shown in the table to the right. Notice that these are also symmetric, so R(m, n) = R(n, m).

Ever overdone it with the sherry on Christmas Eve?

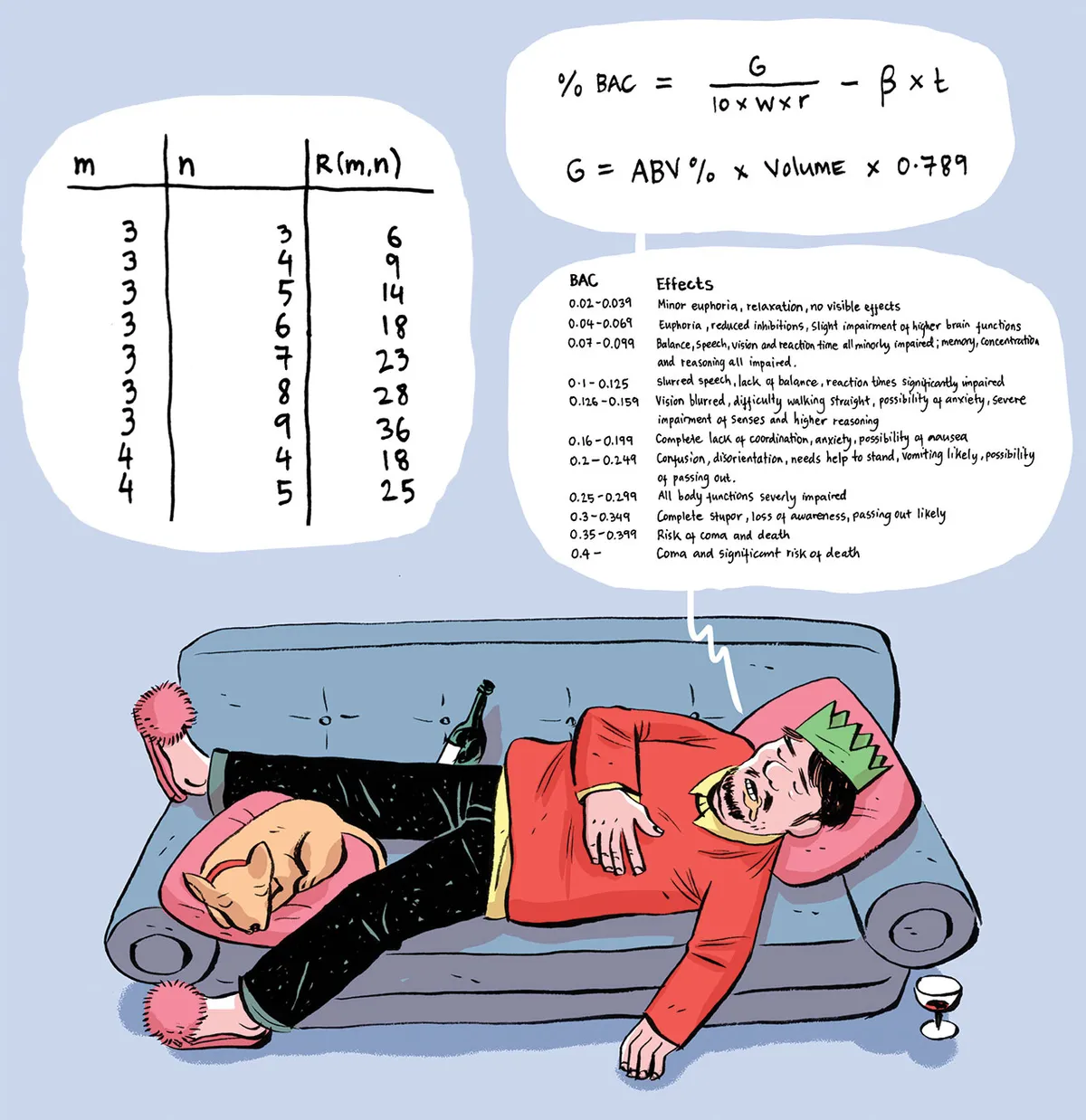
In 1932, Swedish chemist Erik Widmark studied how ethanol (the pure alcohol in your plonk) interacts with the human body, and used his findings to devise an equation for a drinker’s blood alcohol concentration (BAC). The BAC can be used to infer state of drunkenness, allowing the mathematical imbiber to plan their consumption accordingly.

The basic formula is shown in above. G is the amount of alcohol consumed (in grams), t is the time since drinking began (in hours), W is the drinker’s weight (in kilograms), r is the gender constant (0.68 for men, 0.55 for women), and  is the rate that alcohol is eliminated from the body (in %BAC per hour, ranging from 0.01 for people with low tolerance up to 0.035 for seasoned boozers). Grams of alcohol is given by the ‘alcohol by volume’ (ABV) percentage of your beverage times the amount consumed in millilitres times the density of ethanol (= 0.789g/ml).

You can then look up the resulting BAC on the effects table on the left of the image. For example, a man drinks five pints (2,840ml) of 5% beer – that’s 112g of ethanol (2840 x 0.05 x 0.789). If he weighs 90kg and has a moderate alcohol tolerance ( = 0.02) then his BAC after two hours is 0.143. Which is enough to cause a significant risk of missing Christmas dinner.