Snowed In

Nick and his sleigh are stranded in the woods. He is desperate to get back to his cabin in time for Christmas to deliver presents to his children. His usual route would take him in a straight line directly to his cabin, but a snowdrift is blocking his way. Instead, he must take a lengthy diversion.
Nick sledges three kilometres east to the frozen lake, before turning his sleigh 135° clockwise and travelling 1,300 metres to the reindeer stable. According to his sat-nav, he is now 500 metres further south than the frozen lake. Nick then rotates his sleigh 45° clockwise, and travels 1,275 metres to his cabin.
How much further has Nick had to travel due to the diversion?
Cold as Ice

Samuel is captaining an expedition to Antarctica on a ship. A mist has descended and the temperature has dropped to -15˚C, making the journey treacherous. Samuel is aware of an iceberg up ahead, but he is not sure how far it is from the ship.
He stops the ship and sounds his foghorn. He hears the echo of the foghorn 5.2 seconds later. Samuel uses his knowledge about the speed of sound to determine the distance from the iceberg. He knows that the speed of sound at 0˚C is 331 metres per second, and that for every 10˚C below zero the speed reduces by six metres per second.
How far is the iceberg from his ship in metres?
Space Race

Three of the crew on the International Space Station are playing around with miniature spacecraft, aiming them at a target. Alan launches his craft at 1 metre per second (m/s), but doesn’t turn the engine on. At the same time, Bernice launches her craft at 0.5m/s and has its engine on, accelerating the craft at 0.1m/s per second. The two ships hit the target at the same time.
Chester knows that s = ut 0.5at2, where s = distance, u = initial speed, a = acceleration and t = time.
If Chester launches his ship with no initial speed, how much acceleration will it require to take the same amount of time as the other ships did to hit the target?
Square up

Fill the grid using the six coloured shapes. Leave no square blank. You may reuse any of the shapes, and you may rotate them but not flip them. Each shape has a symbol marked on it. The symbols must line up with the ones shown in the grid.
Word games
1. Rearrange the letter groups to make three sciences:
HAN ORO MEC OGY HYD ICS PHY GRA ROL
2. Crack the code to find three sciences:
GNTQTLD, GTYFSD, LJTQTLD
3. Rearrange the letter groups to make three fields of science:
ENY ROL PHY LOG AST OMY HYD OGY RON
Carol’s Conifers

Carol’s Christmas Barn stocks three types of Christmas tree. Scots pines are sold for £25 each, while Norway spruces and Douglas firs are sold for 80% and 50% of this price respectively.
Despite the relatively high price, Scots pines are by far the most popular tree thanks to their high needle retention and fresh fragrance. Carol sold 10 more Scots pines than Douglas firs in the first week alone. In her first week of opening this year she made £1,195, not quite reaching her target of £1,200, but still a satisfactory amount from 59 trees.
How much of this money did Carol make from selling Norway spruces?
Science class
Four siblings are fighting over their toy science kit. Florence has the Bunsen burner and the test tube until Marie snatches one off her. Stephen wants to swap the goggles for the tongs or the Bunsen burner. Marie refuses to swap, but Albert is happy to.
Who ends up with what?
What subject?
Four friends are each starting one of these A-levels this week. Can you match them up? Aidan isn’t taking a language, and Dean isn’t taking a science subject. Chris went for Physics ahead of Chemistry. Brenda had an easy choice as she’d always preferred German to French.
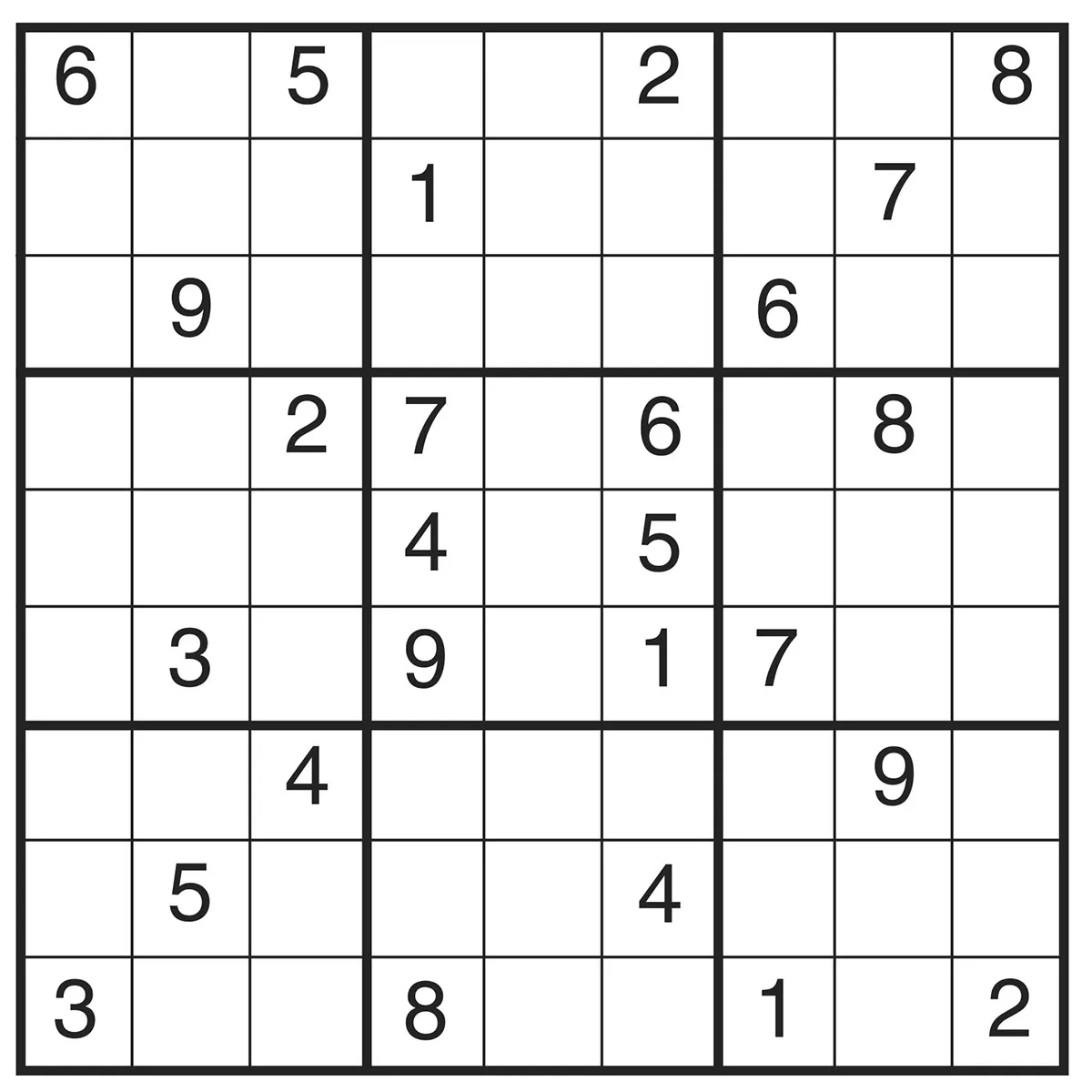
Sudoku
General Knowledge Crossword

Across
1 The property of an object moving away from the middle of rotation (13)
8 Robert, German physician who was a founder of bacteriology (4)
10 A symbol used to express a quantity (7)
11 Another name for the snow leopard (5)
12 Boy's name that derives from the Irish for 'red king' (5)
14 Warm-blooded (11)
15 An amino acid that is a common constituent of proteins (7)
16 Part of a boot or shoe covering the front of the foot (4)
18 Alan, the first US astronaut to travel in space (7)
20 A boundary or restriction (5)
21 A granular or compact mineral found in magnesium-rich rocks (4)
22 Non-flowering aquatic plants that include seaweed (5)
23 Latin expression meaning 'entirely' (2,4)
26 On the ____ of Species, work on evolution by Charles Darwin published in 1859 (6)
27 The prehensile claw of an arthropod such as a crab (5)
28 ____ disease, a virus transmitted to humans by ticks, affecting the joints, heart and nervous system (4)
30 International organisation founded in 1967 to which Indonesia among others belongs (5)
31 Relating to the threshold of consciousness (7)
32 The brightest star in the constellation of Lyra (4)
34 An obscuration of the light of the sun or moon by the intervention of another body (7)
35 Impassive or not showing feelings (11)
38 ____ goose, another name for the Northern gannet (5)
39 The longest river in France (5)
40 Mistakenly (2,5)
41 A large black and white killer whale (4)
42 Prevailing model by which astronomers explain the beginning of the universe (3,4,6)
Down
1 Places where wildlife is protected (12,5)
2 A member of a wandering pastoral community (5)
3 An uncommon thing or incident (6)
4 A gelatinous mass of cyanobacteria once thought to be of meteoric origin (6,4)
5 Partial darkness (5)
6 Possibly the smallest lizard known to science (4-9)
7 Clear, bright green precious stones (8)
8 Border between Earth's atmosphere and outer space named after a Hungarian born physicist (6,4)
9 A cell found in the muscle of the heart (13)
13 Usually the last stage of production in e.g. sodium (17)
17 Most fungi are these type of organisms (13)
19 The practice of capturing, storing, processing and analysing data near the client (4,9)
24 A bear native to South Central China (5,5)
25 US aviator Ed Yost was a pioneer in this activity (10)
29 A society in the US for the singing of choral music (4,4)
33 Another term for advanced or modernistic (2-4)
36 An injection of fluid into the lower bowel e.g. to introduce drugs (5)
37 A slang term in the US for an agent who enforces laws on the illicit production of drugs (5)
Solutions
Snowed In
4,850m
Explanation: Nick has travelled three sides of a trapezium. He moves 1,300m between the frozen lake and the reindeer stable, which is 500m further south. A right-angled triangle can be formed using 1,300m as the hypotenuse. Using Pythagoras’ theorem it can be determined that the reindeer stable is √(1,3002 – 5002) = 1,200m further west than the frozen lake. Nick’s cabin is 3,000 - (1,200 1,275) = 525m further east from where he started. We know that his cabin is at the same latitude as the reindeer stable, 500m further south than the frozen lake and his starting point. A second right-angled triangle can be formed. The direct route to Nick’s cabin is √(5002 5252) = 725m.
Cold as Ice
837.2 metres
Explanation: At – 15˚C the speed of sound is:
331 – (1.5 × 6) = 322 m/s
Samuel hears the echo 5.2 seconds later, so the sound of the foghorn took 2.6 seconds to reach the iceberg.
322 × 2.6 = 837.2 metres
Space Race
0.2 metres per second per second
Explanation: The equation for Alan’s craft is: s = 1t 0t2. The equation for Bernice’s craft is s = 0.5t 0.05t2. The ships travelled the same distance and took the same time, so s and t are the same in both equations.
We can combine them to get:
t = 0.5t 0.05t2
1 = 0.5 0.05t
0.5 = 0.05t
t = 10 seconds and therefore s = 10 metres.
To get Chester’s craft to take the same time, use the equation again:
10 = 0t 0.5at2
10 = 0.5at2
20 = at2
20 = a × 100
a = 20/100 = 0.2 metres per second per second
Square Up

Word Games
1. Hydrology, mechanics, orography
2. Biology, botany, geology (A becomes V, B becomes W, etc)
3. Astronomy, hydrology, phylogeny
Carol's Conifers
£420
Explanation: Assign the letters N, S and D to represent the number of each type of tree. N = Norway spruce, S = Scots pine, D = Douglas fir. Three equations can now be made:
1) N S D = 59
2) 20N 25S 12.5D = 1,195
3) S = D 10
Substitute 3 into 1:
N D 10 D = 59
N = 49 - 2D
Then substitute this equation into 2:
20(49 - 2D) 25(D 10) 12.5D = 1,195
1,230 - 2.5D = 1,195
D = 14, S = 24, N = 21
Carol therefore would have made 21 x £20 = £420 from selling Norway spruces.
Science Class
Albert gets the goggles, Stephen the tongs, Marie the Bunsen burner and Florence the test tube.
What Subject?
Aidan is taking Chemistry, Brenda is taking German, Chris is taking Physics and Dean is taking French.
Sudoku
General Knowledge Crossword

- This article first appeared inissue 371ofBBC Science Focus Magazine–find out how to subscribe here