What is the Fibonacci sequence?
1, 1, 2, 3, 5, 8, 13, 21… The Fibonacci sequence. Every number in the sequence is generated by adding together the two previous numbers. So the next Fibonacci number is 13 + 21 = 34. They are the simplest example of a recursive sequence where each number is generated by an equation in the previous numbers in the sequence.
Hidden inside this sequence is another important number in mathematics: the golden ratio. Denoted by the Greek letter phi, it is a number like pi that has an infinite decimal expansion with no patterns. It starts phi = 1.61803… It’s defined as the ratio of a rectangle of dimensions A x B where the ratio A/B is equal to (A + B)/A.
This is regarded by many artists as the perfect proportion for a canvas. If you divide a number in the Fibonacci sequence by the previous number in the sequence (for example, 5/3) then this fraction gets closer and closer to the golden ratio as you take larger and larger Fibonacci numbers. There’s a formula for the Fibonacci numbers involving the golden ratio that avoids having to calculate all the previous numbers.
There are still mysteries about these numbers. For example, are there infinitely many Fibonacci numbers that are also prime numbers? Like 2, 3, 5 and 13. We only know 51 Fibonacci primes, but could there be an infinite amount?
Why are Fibonacci numbers so important?
They are nature’s favourite numbers. You find them all over the natural world. Count the number of petals on a flower and often it’s a Fibonacci number. (If it isn’t, that means a petal has fallen off your flower, which is how mathematicians get around exceptions).
Cut open a fruit, and often you’ll find a star shape with a Fibonacci number of arms. A banana has a three-pointed star, an apple a five-pointed star, a persimmon an eight-pointed star. Count the cells on a pineapple, and you’ll find several Fibonacci numbers. The seeds in a sunflower also exploit Fibonacci numbers to pack efficiently.
Discover more about maths:
- Was maths invented or discovered?
- What’s the simplest unsolved maths problem?
- Can maths be beautiful?
- Why can’t we predict prime numbers?
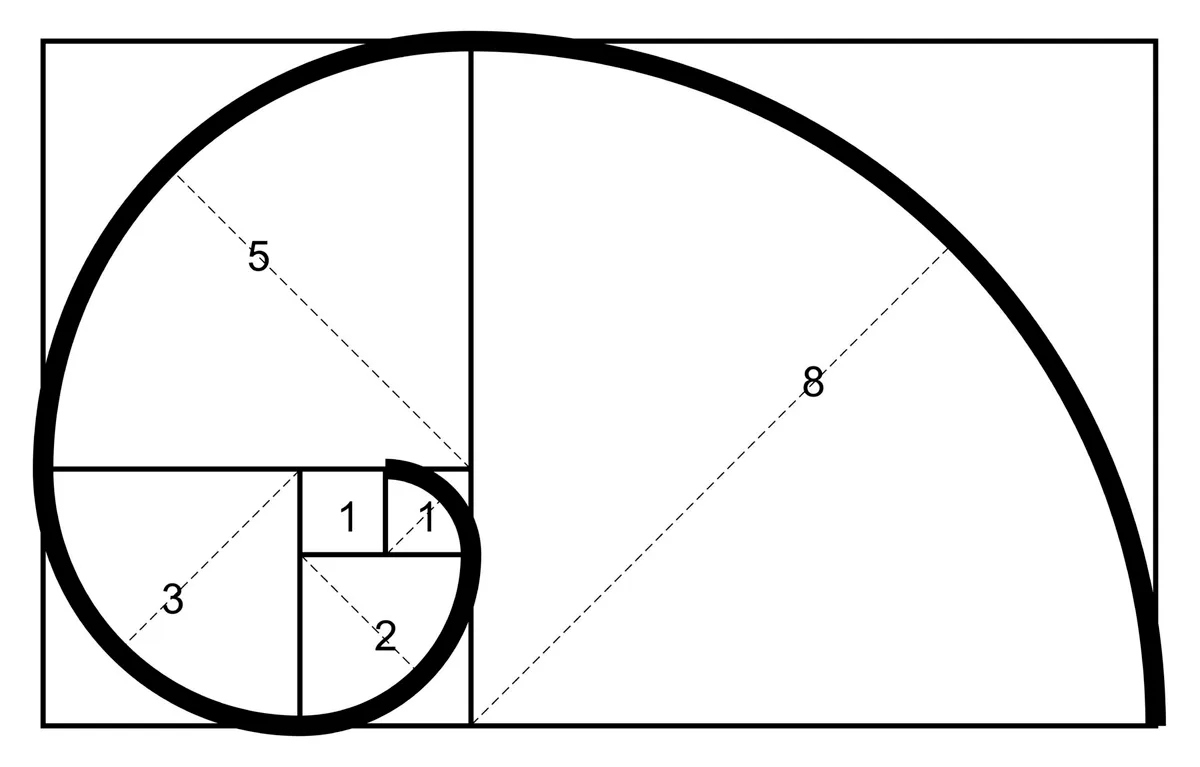
Fibonacci explained that these numbers are at the heart of how things grow in the natural world. Nature uses what it has grown so far to make the next move. If you take squares whose dimensions correspond to the Fibonacci numbers, then it’s possible to arrange them in an expanding rectangle, which explains how they help grow things and why they give rise to spirals.
Fibonacci also explained how these numbers keep track of the population growth of rabbits. If a pair of rabbits take a month to mature before it can give birth to a new pair of rabbits, how many pairs of rabbits will there be each month? The answer is in the Fibonacci sequence.

Who was Fibonacci?
The numbers are named after a 13th-Century Italian mathematician from Pisa, also known as Leonardo Bonacci. He did not come to be widely known as Fibonacci until 1853 when the historian Guillaume Libri began referring to him as Fibonacci, the name being short for filius Bonacci (son of Bonacci).
Fibonacci wrote about these numbers in a hugely influential book called Liber Abaci, published in 1202.
His book was meant as an aid to new ways of doing computation and explains the power of the new Hindu Arabic numerals. He learnt about these new numbers while travelling in North Africa. In Europe, they were still using Roman numerals and the abacus to do calculations. But using the abacus required skill and expertise. It meant that calculation wasn’t something that was available to the common citizen.
Rather than using clumsy Roman numerals, Fibonacci explained how the Indians exploited the numbers 1 to 9 together with the revolutionary new concept of 0 to express numbers efficiently using the place number system. Fibonacci’s book gave the common citizen access to calculation and the ability to record those calculations. This is why the establishment initially tried to ban the incoming numerals from the East.
His book is responsible for kick-starting mathematics in Europe during the medieval period. It’s in the book Liber Abaci that he introduces the sequence of numbers that now bear his name.

Was Fibonacci the first to discover these numbers?
No! It turns out that these numbers should really be named after Indian poets and musicians, who discovered them centuries before Fibonacci. Rather than nature, it was understanding rhythm in music and poetry that was the secret to their discovery.
How many different rhythms can you make on a drum if you combine long and short beats? For example, if a long beat is twice a short beat then here are the number of rhythms you can make of length four: SHORT-SHORT-SHORT-SHORT, LONG-SHORT-SHORT, SHORT-LONG-SHORT, SHORT-SHORT-LONG, LONG-LONG. A total of five different rhythms. A Fibonacci number!
If you wanted to make rhythms of length five then you can take the three rhythms of length three and add a LONG beat to them, or take the five rhythms of length four and add a SHORT beat to them. So there are eight rhythms of length five. The number of rhythms grows according to the Fibonacci rule.
Many modern musicians have enjoyed using the Fibonacci numbers in their work. For example, Debussy uses them in his piece La Mer as does Bartok in his Music For Strings, Percussion And Celesta. There’s even a new form of poetry, called a Fib, where each line has syllables corresponding to the Fibonacci sequence.
- This article first appeared inissue 372ofBBC Science Focus Magazine–find out how to subscribe here
To submit your questions email us at questions@sciencefocus.com (don't forget to include your name and location)